Approximating images with randomly placed translucent triangles, Take 1

April 2, 2010 5 minutes read | 881 words by Ruben Berenguel

Stochastic hill climbing: Sisyphus pushes an image

Last year, Slashdot published this interesting piece of work: Genetic evolution of the Mona Lisa. The idea is to approximate an image by a certain number of semitransparent polygons, randomly chosen. I liked very much the idea, and as every year I try to come up with some Christmas postcard related to maths or programming I gave it a try. So I wrote a LISP version… way too slow. After optimizing a little my code I got a 3x boost… but it was around 3 times slower than the C version I wrote afterwards… Which is still damn slow. But works :) I’ll show here how the algorithm works, and I’ll (officially, it is already available) post the code in a week or so.

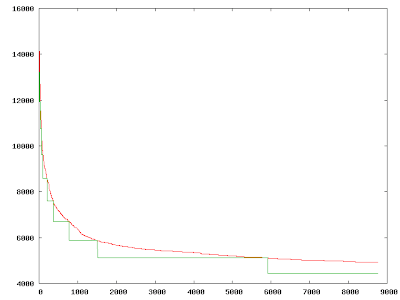
I work just with triangles (it was much easier to write), but the algorithm is quite slow, moreover I need more than 50 triangles to get significative similarities. I have observed some interesting properties of the approximation algorithm. The most significative one, is the asymptotic convergence. Here you can see in red the error of the approximated image (in an arbitrary scale) vs. generation count. As you can see, it is somewhat asymptotic to a stable line. I have made some tweaks trying to at least lower this asymptote, but I didn’t get to it. The green bumping graph is related to a tweak of the algorithm I’ll explain below.

This run took around two days, for around 100.000 generations (estimated count, as generations are not in the “usual” generation count system).

The algorithm works as follows. Given an image we want to approximate, for each generation we do:

If we can add a triangle, try to add a random triangle MaxSteps times. If the image is closer to the original, go on.
Depending on a random factor, either

Changer: Take one of the given triangles of the actual approximation by a random choice and try to change it to a better one, try to do it for a random number smaller than MaxSteps.
Pruner: Try to remove one triangle of the set (try for every triangle)
Mover: Try to move every triangle to every possible position in the triangle list (for every triangle on the list). It starts in random positions in the triangle list, not to bias moving the “underneath” triangles.
Swapper: Try to swap every pair of triangles. As above, but swapping every two triangles.

These last two steps are painfully slow, so they have a probability of happening several times smaller than the Changer.

Repeat

I have set also several thresholds. First, I set a maximum number of triangles, and divide it by 20 (for example). Then, divide the initial error by 8 (for example also, but these are quite good numbers) to have a FitStep, and every time the current fit result for the image is smaller than InitialThreshold-Function(FitStep), increase the number of triangles (if smaller than the total maximum). I added this after realizing that most of the first placed triangles were mostly crap, with this method I try to get for each number of triangles, somewhat like the best possible approximation. This part works quite well, the problem is the later addition of triangles, which is not as good. In the previous plot, the green lines show the triangle add thresholds.

After this, I also realized that random changes for all parameters in a triangle were too random for a change, more so when the image was quite close to the original. Thus I added a Jiggler step, which is chosen randomly instead of Changer, which just moves a little the triangle parameters for every triangle (starting from a random triangle in the list, and for a certain number of tries).

As I said, this algorithm is slow, mostly because of how I started. I needed it to create the Christmas postcard, so I just wrote it and when it worked, I had it running for as long as needed. Now I realize how much tweaking is left to make it somewhat useful (in fact, a quite simple improvement can add a 2x boost…).

Here are two images. One is similar to my Facebook (and some other places) profile image (I recalculated for this post), the other one is what I used for the Christmas postcard you can find in this post.

I’ll post the corrected source soon (it is already in my googlecode repository, but it lacks comments and the most obvious tweaks, and also the shell scripts used to generate the postcard), hope you can wait for it. If you have any suggestions to improve the algorithm, you are really welcome.

Left: approximation (you guessed!).
Above: 74 triangles Below: 156 triangles
Right: original image to aproximate

Thanks to everyone who commented on the Reddit thread. I’ll try to write an improved version soon, with a mix of your suggestions. If you enjoyed reading this, please share it via Reddit, StumbleUpon, Digg or whatever you enjoy using. Thanks!