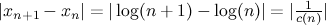Counter-examples, Converging Sequences and Giving Immediate Answers

January 11, 2011 3 minutes read | 537 words by Ruben Berenguel

Next week is the final exam of the course I’m giving, Numerical Analysis. Classes finished before Christmas, and this week is for students questions. I had one of these sessions this morning, when a pair of students came with a few questions related to the problems I solved on the blackboard.

All were quick to solve, until one simple question arose, concerning a trivial problem in Calculus 1 (or Analysis 1, as we name it here). The problem is:

Given a sequence , the fact that for any does not imply that is a converging sequence.

The statement is clear, and as a fact, it is something I’ve known for 9 and a half years, since my first semester of Mathematics. But they were not convinced. And I needed a counterexample for it to remove it. But I was out of ideas: out of the cold I just can’t find counterexamples unless I’ve already thought about that problem before (as a generic property, some times I can do it).

This is something I was already aware, but this morning was a big hit. I kept working during the day on my usual tasks, but on my way to take the train back home I had a few minutes to spare a thought or two while going there. But just took me 1 minute, from my office to the university side door.

Let 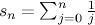, then , which satisfies the conditions of the statement, and 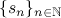does not converge.

Anyway, I was not happy with this solution, as it was over our level in our first course. A more basic example not involving series should be easy to get. In the afternoon I had asked a friend the question through GTalk, but he was away, and as we picked it up again he wanted to know if I had some solution to it. I told him that indeed, but I was not happy. He then asked if the partial sums of the harmonic series were not enough (this is another name for my sequence ). As I told him that they were not, he suggested using logarithms. Aha!

Let , then by applying the mean value theorem,

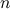where is a value between and . And 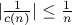, which implies that this sequence also satisfies the conditions and clearly diverges.

In conclusion, I was able to find the counter-examples, but it took me far more time than needed. Is speed that important?

Of course, all great mathematicians I know are able to answer these kind of questions (giving simple counter-examples to trivial questions, or finding trivial models to work on before moving to the big task), but does this come from experience or is just innate?

While thinking about this problem, I remembered a book recommendation I was given a long time ago: Counterexamples in Analysis (buy on Amazon link). I never took the chance to read it… Maybe the time has arrived!